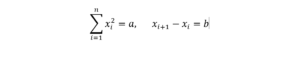كتبهُ لمجلة (Spektrum) الألمانية: هاكان برونكه (Hagan Brunke)
نشر بتاريخ: كانون الثاني 2018
ترجمة: حسام زيدان
تدقيق: نعمان البياتي
تصميم الصورة: حسام زيدان
المصدر: النسخة المطبوعة من مجلة (Spektrum)، العدد الخاص بشهر كانون الثاني 2018، ص78، 79
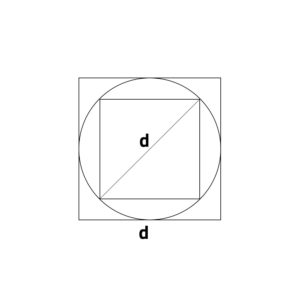
المعادلة المشهورة a^2+b^2=c^2، والتي تربط طول الضلعين a وb مع طول الوتر c بعلاقة واحدة، منسوبة لفيثاغورس (570 ق.م-510 ق.م)، لكنها تعود لحسابات مثلثية لعلماء رياضيات بابليين سبقوه ب 1300 عام؛ وكانوا يعرفون كذلك الطريقة التقريبية لحساب الجذر التربيعي والمنسوبة لهيرون الاسكندري (في القرن الأول بعد الميلاد تقريباً)، وهكذا وبحسب لوح يعود لتلك الحقبة ومكتوب بالخط المسماري، فإن تلميذاً من بلاد الرافدين أعطى القيمة الصحيحة تماماً للجذر التربيعي للرقم 2 بخمسة مراتب بعد الفارزة والتي هي 1,41421. حيث كانت القيمة مكتوبة بالنظام الستيني الشائع استخدامه آنذاك بالشكل التالي: 1,24*51*10، أي ما قيمته: 1+24*〖60〗^(-1)+51*〖60〗^(-2)+10*〖60〗^(-3). . نظراً لهذه الدقة في الحساب فإنه من المثير للعجب أنهم استخدموا المعادلة 3r^2، لحساب مساحة دائرة ذات نصف قطر مقدارهُ r، وذلك بدلاً من استخدام القيمة التقريبية للعدد الثابت باي π والتي تساوي 3,1415 تقريباً. من الممكن أن البابليين قد قدّروا قيمة مساحة الدائرة للقيمة المتوسطة لمساحتي مربعين، أحدهما يحيط بالدائرة والآخر محاط بها:
مساحة المربع الخارجي هي d^2 (حيث أن d=2r ويمثل قطر الدائرة) ومساحة المربع الداخلي هي d^2/2؛ القيمة المتوسطة للمساحتين: (3d^2)/4=3r^2. ، إلا إنه لا توجد مصادر مكتوبة تثبت صحة هذه النظرية.
كان علماء الرياضيات في بلاد الرافدين قادرين أيضاً على حساب مساحات أشكال هندسية معقدة، كوثيقة مميزة ومثيرة للإعجاب تثبت هذه الإجادة، يمكننا إيجادها في إحدى ألواح المتحف البريطاني. صحيح أنهُ لا يعطي لنا سوى هيكلية تلك الأسئلة وليس طرق حلها، ولكن مما لا شك فيه أن تلك الأسئلة قد حُلَّت.
للممارسة اليومية كانت هناك قوائم العلماء (ملخصات أنشأها علماء ذلك العصر: المترجم) متاحة، والتي تقابل في استخدامها كتيّبات الملخصات الرياضية والتقنية المعروفة اليوم. إنها تحوي على جميع أنواع القيم المميزة في مجالات الهندسة، التقنية والإدارة بالإضافة لمجالات أخرى. في هذه القوائم نجد على سبيل المثال: <<20: قطر الدائرة>> و<<5: القيمة المميزة للدائرة>>، حيث إن العدد 20 بالنظام الستيني يقرأ 20⁄60، أي 1⁄3 وهي القيمة البابلية لعدد 1⁄π. بالمقابل فأن 5 بالنظام الستيني تقرأ 5⁄(60=1/12)، وهي القيمة البابلية لعدد 1⁄4π. هذه القيَم هي العوامل التي كان يحسب من خلالها قطر دائرة بواسطة المحيط بالإضافة الى مساحتها من خلال مربع المحيط. نجد هنا أيضا مختلف الطرق، التي تساعدنا اليوم على سبيل المثال في تقدير تكاليف البناء.
الوثائق الرياضية الأولى لبلاد الرافدين نجدها في نصوص ألواح مسمارية تعود لأواخر الألفية الرابعة في أوروك، حيث يتم حساب مساحات لحقول مستطيلة الشكل وذات الشكل الرباعيّ الأضلاع غير المنتظم. الطريقة التقريبية التي استخدمها سكان بلاد الرافدين لتحديد المحتوى، كانت عبارة عن عملية ضرب القيمة المتوسطة لطول الضلعين المتقابلين، تماماً كالطريقة التي استخدمها الرومان بعد 3000 سنة.
حتى الأشياء التجريدية لم تكن غريبة عن الرياضياتيين البابليين، وبهذه الطريقة استطاع أحد العلماء حل نظام مكوّن من معادلات تربيعية ومعادلات خطية؛ هذا ما يظهره اللوح المسماري أدناه، حيث تحتوي على الحل الكامل للمعادلات:
x^2+y^2=a و y=x+b بقيمٍ عددية محدد: a=1300و b=10.
في الترجمة التالية قمت بإكمال النص وتحويل الأعداد من النظام الستيني إلى النظام العشري.
1. لقد قمت بجمع مساحة مربعين (والنتيجة هي) 1300.
2. (أحد) أضلاع المربع يزيد عن الضلع (الآخر) بمقدار 10.
3. تُقسِم النصف من 1300 (من السطر الأول).
4. ثم تكتب (النتيجة) 650.
5. تُقسم النصف من 10 (من السطر الثاني).
6. ثم تَضرِب (النتيجة)5 (بالنتيجة)5.
7. تَطرَح (النتيجة) 25 من 650 (من السطر الرابع).
8. (من النتيجة)625 (يكون) 25 (هو) الجذر التربيعي.
9. تَكتُب (هذه) ال 25 مرتين.
10. تَجمَع ال 5 التي قُمت (في الخطوة 6) بتربيعها مع أحد الـ 25 (من السطر9).
11. و (النتيجة) 30 هي ضلع المربع (الأول).
12. تَطرَح (الـ) 5 (التي قُمت في الخطوة 6 بتربيعها) من الـ 25 الثانية (من السطر 9).
13. و (النتيجة) 20 هي الضلع الثاني للمربع.
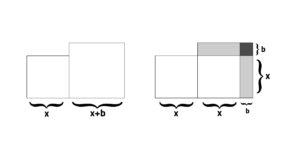
يمكن تفسير خطوات الحل كالتالي: لدينا مربعين بأطوال أضلاع x وx+b (المجهولة الطول)، ويمكننا اعتبار أن المربع الكبير يتكون من المربع الصغير “وبقيّة”(أي أنّ مساحة المربع الكبير هي بقدر مساحة المربع الصغير مع بقاء جزء الفرق من المساحة-المترجم). الجزء المتبقي يتكون بدوره من شريحتين بلونٍ رماديّ فاتح بعرض مقداره b وطول مقداره x، بالإضافة إلى مربعٍ صغير ذي لون رمادي قاتم بطول ضلع مقداره b.
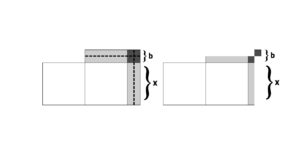
يتم في السطر الثالث طرح النصف من المساحة الكلية (تحديداً a والتي مقدارها هنا 1300). هندسياً من الممكن تحقيق ذلك، من خلال إبعاد مساحة بمقدار نصف شريحة، من كلا الشريحتين ذي اللون الرمادي الفاتح بالإضافة الى ربعين من مساحة المربع الصغير ذي اللون الرمادي القاتم. بذلك تكون مساحة الشكل الناتج هي a/2، هنا بمقدار 650.
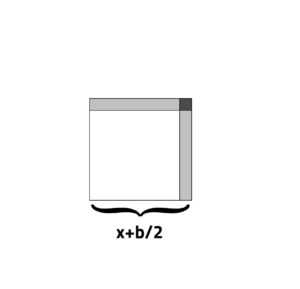
كل من الجزأين المتبقيين من المربع ذوي اللون الرمادي الداكن يحمل طول ضلع مقداره (كمثال عددي محدد b/2) (=5) وبالتالي بمساحة مقدارها (〖b/2〗^2) (=25). يتم في الخطوة 7 استبعاد أحد الجزأين من الشكل الناتج (تَطرَح 25 من 650)، على سبيل المثال الجزء الخارجي؛ المتبقي يكون عبارة عن مربع بطول ضلع مقداره x+b/2:
مساحته هنا هي 650-25=625، التي يتم منها في الخطوة 8 حساب الجذر التربيعي. النتيجة (هنا 25) هي طول ضلع المربع، أيx+b/2 . هذه النتيجة يتم كتابتها مرتين (الخطوة 9) ومن ثم إجراء عمليتين مختلفتين: عملية جمع b/2 (الخطوة 10) تعطي x+b، والتي هي طول ضلع المربع الكبير(السطر 11)؛ بالمقابل فإن عملية طرح b/2 (الخطوة 12) تعطي قيمة x، والتي هي طول ضلع المربع الصغير (السطر 13).
طريقة الحل هذه، تصلح أيضاً عند تعويض أعدادٍ أخرى، بدلاً من الأعداد المحددة (1300 لـ a و10 لـ b) التي حُلّت المسألة بها، ولا يوجد خلاف اليوم بأن الرياضياتيين البابليين كانوا على علم بهذه الحقيقة؛ وكانوا قد استخدموا القيّم العددية المحددة أشبه بمتغيرات، هذا ما أثبته أوتو نويكباور (Otto Neugebauer)، الرائد في مجال رياضيات الألواح المسمارية، مسبقاً منذ ثلاثينات القرن العشرين.
لقد استطاعوا أيضاً إيجاد صيغة عامة للمسألة المذكورة: المطلوب ايجاده لم يكن مربعين فقط، بل عدد n من المربعات، التي يكون فيها طول ضلع كل مربع، أكبر من سابقهِ بمقدار b ومساحته الكلية منصوص عليها. في طريقة التدوين المعاصرة تكون الصيغة كالتالي:
 Iraqi Translation Project لأن عقوداً من الظلام الفكري لا تنتهي إلا بمعرفة الأخر الناح..لابد من الترجمة
Iraqi Translation Project لأن عقوداً من الظلام الفكري لا تنتهي إلا بمعرفة الأخر الناح..لابد من الترجمة